株価関数の推計
続いては、割引キャッシュフローモデルを元に、過去20年間の関係から株価関数の推計を実施する。具体的には、株価をP、直近キャッシュフローをCF、今後のCF成長率をg、割引率をrとしたとき、以下の計算式で株価を計算するモデルである。
このモデルは、一般に個別企業の理論株価を算出するものであるが、今回はマクロの株価指数と総所得の関係を確認する理論として利用する。具体的には、マクロの総所得を名目GDPとして、今後のCF成長率の代理変数を名目GDP成長率、割引率の代理変数を長期金利とすれば、マクロの株価指数は名目GDPと長期金利で説明できることになる。そして、CF成長率の代理変数となる名目成長率が高ければ理論株価は上昇し、割引率の代理変数となる長期金利が上昇すれば、理論株価は下がることになる。
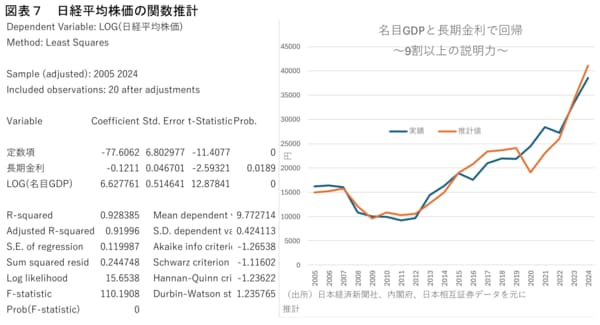
実際、平成7年の経済白書では、加重平均株価を名目GDPと長期金利で回帰し,推計値と実績値の推移を比べた分析をしている。そこで、今回も過去20年間の日経平均株価(年度データ)を元に同様の分析を試みた(図表7)。結果は以下の通りであり、まず自由度調整済み決定係数が0.92と非常に高い説明力を有することがわかる。そして、推計値と実績値の推移を比べると、2015年度までは似通った動きを示していた両者は、中国リスクや英国EU離脱があった2016年度やロシアのウクライナ侵攻が起きた2022年度には推計値が上昇する中で実際の株価が低下した一方、コロナショックが起きた2020年度は逆に推計値が著しい低下を示す中で実際の株価は上昇してきたことがわかる。
とはいえ、高い決定係数を有していることからすれば、こうした過去20年にみられた両者の深い関係は、今後の名目GDPや長期金利の予測値を今回推計した株価関数に代入することで、将来の株価を見通せる可能性があることを示している。