インフレ、マーケットetc.アメリカでは単純計算は成り立たない
アメリカはこうはいきません。コンスタントにインフレ率があり生活費は年々確実に上昇していきます。また、401(k)などの企業内積立プラン、個人運用プランなどで老後資金を運用するのは広く普及していますので、リスクをとっての投資がなされています。寿命を全うするまでの数十年以上もの期間、市場がどのように動くかは誰にも分かりません。資産のほうもいろいろ動けば、生活費も一定でない…簡単に割り算をするという単純計算では対応できない世界です。
そんなアメリカでは、運用しながら引き出しつつ資金枯渇なしに寿命を全うできるシナリオを、統計的に探っていくモンテカルロ法という手法が一般的に使われています。一例を紹介すると、こんな感じです。
図2.モンテカルロ法によるシミュレーション
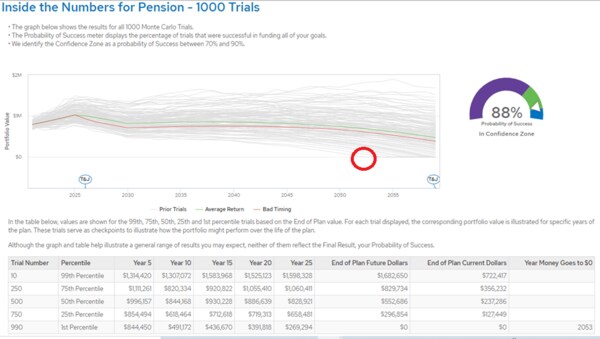
ここでやっていることは、この人の持っている投資ポートフォリオのリスクレベルに応じて、実際にありそうな1000通りのシナリオをつくります。その一つ一つのシナリオには、今から寿命全うまでの間の一年一年がどのような市場の状態であり、保持している投資ポートフォリオにおいて利回りがどのようになるかを想定しつつ、同時に必要な生活費のインフレ成長も反映させながら資金の切り崩しも行い、資産がどのように減っていくか(場合によっては増える場合もあり)をプロットしていきます。
上のグレーの線一つ一つが1000の異なるシナリオに相当します。一番上に位置する最善ケースは、市場の好調が続き、生活費の切り崩し額を超えて毎年の利回りが出るため、資産が大きく成長して終わるバラ色のケースです。反対に、一番下に位置する最悪ケースは、市場の不調が続き、2051年あたりで早期資金枯渇となっています(赤の丸をつけたあたりです)。
こうやって行った1000回の想定ケースのうち、何回で資金枯渇なしに寿命を全うできたかの確率を求めたものが成功確率です。上の場合は88%という結果でした。1000回中、880回は資金枯渇がなかったことを示しています。
いったい、裏ではどんな計算をしているのかと思いますね。私も深くは理解できませんが、少し調べてみました。よくコンピュータなどの歴史で名前が出てくるジョン・フォン・ノイマンという人がいますが、モンテカルロ・シミュレーションはこのノイマンとその研究仲間が発案した手法だそうです。乱数を利用して事象を確率的にシミュレーションする方法で、この方法は確率的ゲーム(=賭け)として数学的に定式化できることから、ギャンブルの街にちなんで「モンテカルロ法」と呼ばれるようになったそうです。といっても漠然としていてよく分かりませんけど、ここでのキーワードは「乱数」です。「乱数」とは、完全にランダムで何の規則性も意図もない、完全に適当な数字です。
シミュレーションの背景にある「ランダム・ウォーク理論」とは
なぜそれが投資運用のシミュレーションに広く使われるか、ですが、株式市場の値動きがランダムであるという考え方と結びつくからです。
株式市場のランダム・ウォーク理論というのをお聞きになったことはありますか? 株価をはじめとする金融商品の値動きには規則性が無く、明日の変動は過去の変動とは一切関係がなく、ランダムであるという理論です。この理論では、今後の値動きを予測するうえで過去の値動きは参考にならないと理解します。つまり、今年〇〇が大変伸びで調子がよいから、来年もこの調子で行くだろう…といような予測は全くつかず、今年と来年の成績は全く関係がなく、それぞれがまったくランダムであるという考え方です。実際、過去の株式市場の値動きを見ていると、本当にランダムに見えるので体験的にも納得のいく理論です。
ランダムとは言うものの、株には期待利回り(リターン)とリスクという考え方がありますね。よくハイリスク・ハイリターン、ローリスク・ローリターンといいますから、このリターンとリスクは関連し合ってもいます。それがランダムとはいったいどういうことでしょうか?
例えば下は、2021年9月にバンガード社が出した10年予想です。
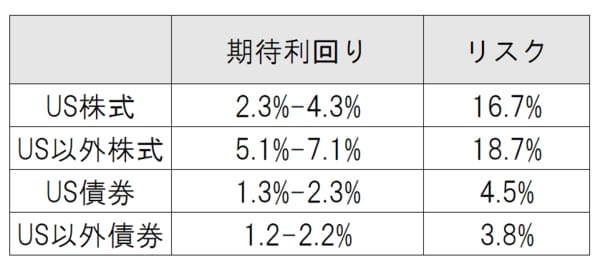
US株式(アメリカ株式市場全体)は、期待年利回り2.3%-4.3%の間(ここでは範囲で提示されていますが、以下では話を簡単にするために中間値3.3%を期待利回りとして扱います)、リスクは16.7%です。この意味するところは、利回りとして最も確率の高い値は3.3%であるが、ただしリスク(ブレ幅)は16.7%であるので、いいとき20.0%(上にブレた場合:3.3%+16.7%)にまでなることもあれば、ひどいと-13.4%(下にブレた場合:3.3%-16.7%)になる可能性があるということを示しています。そしてこの一定の範囲の間で、中央値を中心にしながらも、年々の利回りはランダムにあっちこっちに動き回ると考えるわけです。統計学的には、利回りがブレ幅1倍(±16.7%×1)である-13.4%から20.0%の範囲のどこかになる確率は70%弱で、ブレ幅を2倍(±16.7%×2)にした範囲-30.1%から36.7%のどこかになる範囲は95%というふうになりますが、ここではその話は突き詰めません。ポイントは、最も確率的に高い中央の期待値を中心に、悪くもブレるし、よくもブレる可能性があり、あっちこっちにランダムにブレるということです。
モンテカルロ・シミュレーションでは、この期待値であるリターンとリスク(ブレ幅)の情報に基づいて、その人の投資ポートフォリオの中身に照らし合わせながら、与えられた範囲内でランダムにその年その年のリターンを選び(乱数発生により)、ランダムに動く値動きを疑似的に作り出していきます。ランダムに動く将来の市場をシナリオ化していくわけです。それを1000回繰り返したのが図2です。
モンテカルロ・シミュレーションにおいて、成功確率はどれくらいが適切か
図2では成功確率が88%と出ていますが、これをどうとらえましょう。88%の成功確率というと12%は不成功、つまり寿命より前に資金枯渇があったということを意味していますから、困ったことだ!と考えがちですが、実はそんなことはありません。資金枯渇のケースは、通常リタイヤメントの早いうちか、遅くとも中期までには株式市場の暴落や継続的な不調を経験するケースです。システムは、それにもかかわらず設定された通りの生活費を引き出し使い続けることを前提にして確率計算しています。ところが、実際の生活では、あまりの市場不調があった場合には、「これはちょっと方向修正せねばならない」と察知し、数年は引き出しを最小限にして暮らすとか、生活の縮小を計って生活費を永久的に下げるなどという調整も大いに可能です。
実際、プラニングをするときには、生活費を固定費と変動費に分け、変動費部分に含まれる余暇、趣味、旅行などは必要な時はカットできるように仕分けしておきます。80%台の成功確率であるならば、好ましくないシナリオに発展した場合も、このような調整をすれば資金枯渇なくやっていける可能性が高いと考えてよいと思います。
成功確率のとらえ方としては、以下のようなガイドラインがあります。70%以下だと不確定性が高すぎ、市場ショックがあった場合には軌道修正などしたとしても対応が難しい可能性があるととらえます。まだリタイヤ前ならばもう少し貯める額を増やしたり、リスクを上げて運用成績向上を計ったり、最初から生活費の削減などの対策をとるなどして成功確率を上げる努力をします。
反対に成功確率が90%以上だと、ちょっと「貯めすぎ・行き過ぎ」の度合いが高いと判断されます。大変に保守的で、最後まで資金枯渇しないどころかある程度残して逝きたい…というような方には、このレベルが適切かもしれませんが、ふつうの方には保守的すぎる感があります。それほど貯めすぎなくともよいかもしれない、今に楽しむことや生活を豊かにするためのことにお金を使うということも考えてもいいかもしれないことを意味しています。
この間の成功確率70%から90%の範囲が「適切」と判断されます。確率的には資金枯渇の可能性も算出されているが、それは軌道修正によって対応可能な範囲であり、このままの状態でやっていってよしと判断される範囲です。資金枯渇はしないが、寿命全うする時に残りすぎもしないレベルを狙う感じです。年齢も考慮するべきかと思います。比較的若いうちは70%台でも十分かもしれませんが、だんだんとリタイヤメント年が上がるにつれてできれば85%程度を狙い、リタイヤメント中期を過ぎたら90%程度を狙っていくほうが安心というような進め方をしています。