① バーゼル規制とリスク・ウェイト
本連載で何度となく説明してきたが、銀行などの預金取扱機関はバーゼル規制と呼ばれる自己資本比率規制の適用を受けている。規制自体はバーゼルⅠ時代と比べ、(無駄に)複雑化しているフシもあるのだが、それでも基本的に次の2本の計算式を抑えておけばよいだろう。
自己資本比率=自己資本÷リスク・アセット…①
信用リスク・アセット=与信相当額×リスク・ウェイト…②
①式は、自己資本比率を計算するための基本式だ。「自己資本」や「リスク・アセット」について論じ始めると、それだけで書籍が1冊や2冊書けるほどの膨大な量の論点があるが、自己資本やリスク・アセットの定義がどんなに複雑になったとしても、この計算式自体は変わらない。大雑把に、「自己資本比率を高めるためには、自己資本を増やすか、リスク・アセットを減らすか、そのどちらかしかない」、「多くの金融機関にとって、リスク・アセットのなかで最も大きい項目は信用リスク・アセットである」、と理解しておけばよいだろう。
そして、その信用リスク・アセットの算出方法を示したものが②式である。信用リスク・アセットは、基本的に「与信相当額」を計算したうえで、「リスク・ウェイト」を乗じて求められる。与信相当額(エクスポージャー)とは、通常の貸出金などであれば貸出額、債券やセカンダリーで取得した金銭債権などについては償却原価、株式などであれば取得原価であり(※標準的手法を適用する国内基準行の場合)、ある意味でわかりやすい。
② オフバランス項目とは?
ただ、金融機関は現実に資産、負債、取引などが財務諸表に計上されていない段階でも、何らかのリスクを負うことがある。たとえば「当座貸越契約」のように、現時点ではまだ貸付が発生していないものの、もしかしたら将来的に貸付が発生するかもしれない項目などがこれに該当する。そして、こうした財務諸表に表れてこないリスクについても、バーゼル規制上はエクスポージャーとして認識しなければならないこととされている。これが「オフバランス取引」だ。
ただ、オフバランス取引の場合は、オンバランス項目と違い、まだ実際に取引などが発生していない状態であるため、契約上の金額をそのまま与信相当額とするわけにはいかない。リスクはオンバランス項目と比べて低いと考えられるからだ。そこでオフバランス取引については信用リスク・アセットを計算する前に、まずは与信相当額を計算しなければならない。
バーゼルⅡ規制下では、このオフバランス取引については想定元本額に対し一定の掛目を掛けたものが「与信相当額」とされていた。その概要を抜粋すると図表1のとおりだ。
図表1 バーゼルⅡ規制下の主なオフバランス取引の「掛目」
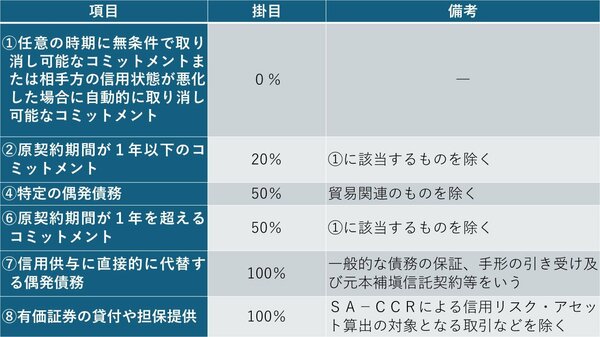
これによると信用供与に直接的に代替する偶発債務や有価証券の貸付取引などは100%の掛目を適用しなければならないとされていたが、それ以外のコミットメントなどについては0~50%の掛目を適用すれば良く、とくに旧告示第78条第1項第1号に定める「任意の時期に無条件で取り消し可能なコミットメント」、「相手先の信用状態次第では取消可能なコミットメント」については掛目が0%、つまり与信相当額がゼロと計算され、そもそもリスク・アセットどころか与信相当額を算出する必要性すらなかった。
③ バーゼルⅢで最低10%の掛目が必要に!
ただ、これがバーゼルⅢ最終化によって、図表2のように掛目が改定された(※一部項目には経過措置や例外としてのゼロ%が設けられているが、本稿では詳細は割愛する)。
図表2 バーゼルⅢ規制下の主なオフバランス取引の「掛目」
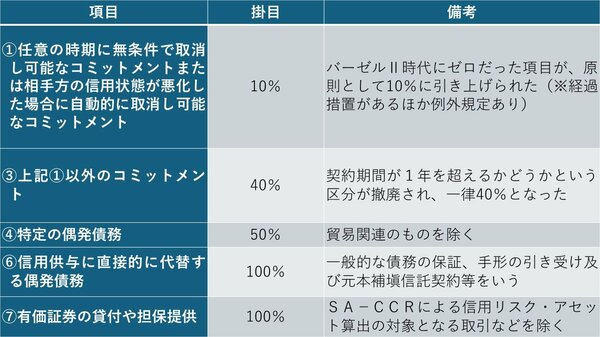
これにより、(一定の例外を除けば)基本的にオフバランス取引はすべて10~100%の掛目を乗じることが求められるようになり、信用リスク・アセットがゼロになることは考えづらい。
④ 組合とキャピタル・コール方式
そして、現代の金融機関が貸出金や国債、地方債といったシンプルな投融資のみならず、プライベート・アセットを含めたさまざまな形態の投融資を行わざるを得ない中で、オフバランス取引との関係で問題となり得るのが組合等出資だ。
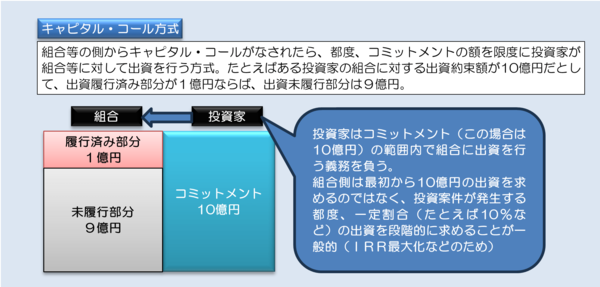
組合(匿名組合や投資事業有限責任組合など)は近年、いくつかのプライベート・アセット投資において利用されるスキームだが、その多くは内部収益率(IRR)を高めるために、キャピタル・コール方式を採用している。キャピタル・コール方式とは、ファンド側が実際に投資を行うなど、資金需要が生じるタイミングで投資家に資金を払い込むよう要求する方式で、一般に投資家は出資約束金額(コミットメント)の範囲でキャピタル・コールに応じる義務を負う。
たとえば、ある投資家がある組合に10億円出資すると約束していたとする。多くの場合、組合側はいきなり10億円の全額の出資履行を求めるのではなく、組合側で具体的な投資案件が発生したタイミングでコミットメントの一定割合(たとえば10%=1億円)を払い込むように要求する(図表3)。
図表3 キャピタル・コール方式
問題は、リスク・アセットの計算だ。
この事例でいえば、出資履行済みの1億円部分については、投資家から見てオンバランスのエクスポージャーであり、ファンドのエクイティ出資などの考え方に基づき、1億円を与信相当額(エクスポージャー)としたうえで、組合の投資内容などに応じて計算した加重平均リスク・ウェイトを適用してリスク・アセットを計算すれば済む。
しかし、問題は未履行部分の9億円だ。
これについて、金融庁のQ&A(2022年7月15日公表版)第78条-Q7には、こんな趣旨のことが書かれている(大意を変更しない範囲で語句の順番を入れ替えてある)。
「(組合等出資金の出資未履行部分は)一定額を限度に与信先からの要求に応じて資金を提供する点でコミットメントと同様と考えられることから、出資枠から既に出資した額を控除した未引出額の与信相当額を算出するに際しては第78条第1項のコミットメントに係る掛目を当該未引出額に乗じることとします。」
具体的には、同第1号に規定する「任意の時期に無条件で取り消し可能なコミットメント」に該当すれば10%を乗じた額(つまり9億円×10%=9000万円)、それ以外のコミットメントに該当すれば同第3号に従い40%を乗じた額(つまり9億円×40%=3億6000万円)が与信相当額となる。バーゼルⅡ時代に「組合契約は任意の時期に無条件に取消可能だ」と判断していた銀行は、これまで与信相当額を算出するに際し、出資未履行部分に0%の掛目を乗じていたと思われるが、今後は最低でも10%の掛目を乗じることが必要となる。
また、もし当該組合契約について「任意の時期に無条件で取消可能」ではない、と判断するならば、乗じるべき掛け目は10%ではなく40%となる。
⑤ リスク・ウェイトは何%を適用すれば良いのか?
しかし、ここでもうひとつ、問題が出てくる。
信用リスク・アセットは、与信相当額にリスク・ウェイトを乗じなければならないのだが、そのリスク・ウェイトはいったい何%を適用すれば良いのか、告示にもQ&Aにも規定が設けられていないのだ(図表4)。
図表4 リスク・ウェイト問題
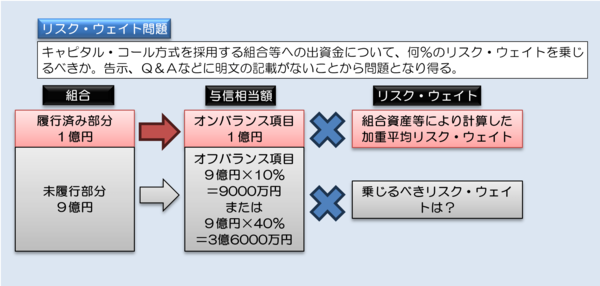
こうした場合、乗じるべきリスク・ウェイトはいったい何%と考えるべきだろうか。出資未履行部分はその名の通り、出資が履行されていない部分であり、したがって投資も行われていないため、加重平均リスク・ウェイトも算出しようがないからである。
⑥ 金融庁の行政の不備?…実務的には「その他の100%」が現実的
この点について、著者もずいぶんと調べてみたのだが、その限りにおいて、明確な答えは見当たらない。
ただ、これに関しては、各金融機関へのヒアリング内容と著者自身の見解を総合すれば、次の3つの考え方があり得る。
1つ目は、履行済み部分(図表4でいうところの1億円)に相当するリスク・ウェイトを、未履行部分にもそのまま当てはめる、という方式。
2つ目は、未履行部分については「株式及び株式と同等の性質を有するものに対するエクスポージャー」とみなし、250%ないし400%のリスク・ウェイトを適用する、という方式。
そして3つ目が、未履行部分については「その他のエクスポージャー」として100%の規定を適用する、という方式だ。これらをまとめたものが図表5である。
図表5 出資未履行部分のリスク・ウェイトをどう考えるか
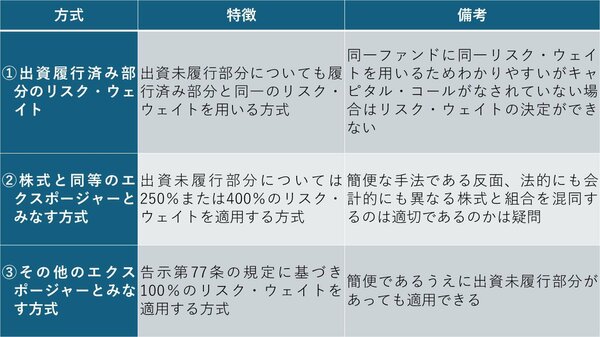
1つ目の方式は現在の組合の投資内容から将来のリスク・アセットの構成を推察する、というものであり、非常にわかりやすいが、この方式には欠点もある。組合に出資をコミットした直後に決算を迎えた場合などのように、極端な話、キャピタル・コールがゼロだったとすると、適用すべきリスク・ウェイトが決められなくなることだ。
一方で、2つ目の方式は、組合自体を株式と似たようなものだとみなし、株式と同じ250%ないし400%のリスク・ウェイトを適用するというものだが、個人的に組合出資を株式と同等の性質を有するものとみるのは無理があると思う。法的性質も会計処理も全く異なるからだ。
そこで、著者自身がおすすめするのが、3つ目の方式だ。
銀行告示第77条には「右記以外のエクスポージャー」として、こんな規定が設けられている。
「第五十五条から前条までの規定に該当しないエクスポージャーのリスク・ウェイトは、百パーセントとする。」
告示第55条から第76条の5までの条文のどこを見ても、「組合の出資未履行部分のリスク・ウェイト」に該当する規定が設けられていないわけだから、正直、これで良いのではないだろうか。このあたり、もちろん、本来ならば金融庁がQ&Aなどを改正し、明文の指針を示すべきであろうと思われる。しかし、少なくとも本稿作成日時点において規定がない以上、これは金融庁による行政上の不備であり、したがって、無駄に悩まず最も現実的で簡便な処理とせざるを得ないと思うのだが、いかがだろうか。












